“I just read from Algorithms to Live By“, “it was mentioned in Algorithms to Live By that”, “there’s a chapter about this in Algorithms to Live By” and variants thereof have been a regular part of my vocabulary as of late. I borrowed this gem from an acquaintance on a whim sometime ago, because it seemed like it might be interesting. It turned out to be pretty great for the most part. It was also apparently listed as one of the best Science books of 2016 by Amazon and probably got a bunch of other such acknowledgements, but I wasn’t really aware of any of these.

Algorithms to Live By is a book about applying insights from computer science to common real-life problems – mostly insights stemming from theoretical computer science, the sort that studies questions such as “what can be computed” and “which problems can be solved efficiently (according to a specific technical definition of ‘efficiently’)”. It’s less a book about computers as physical machines, the internet, programming or other more engineer-level things that people might associate with the term ‘computer science’. Essentially, the book deals with using ideas from the field of algorithmics to make the best possible kinds of decisions in situations of uncertainty, limited resources and intractable complexity.
I imagine the book’s premise may sound preposterous to many people with a background in more human-oriented fields, like the humanities or social sciences, but that’s hardly the case. Rarely do the authors claim that they can present a method for finding the right answers. In fact, it’s a recurring theme throughout the book that those are often even theoretically unattainable (in polynomial time by a deterministic Turing Machine, at the very least), but that computer science can at least help us make the very best guesses.
One of the book’s strong points is that it’s very approachable to people from different backgrounds. Yours truly happens to be an undergraduate student in computer science (although I’ve regrettably had too little time for that subject as of late), and I was at least familiar with the basic mindset of the book and, on a surface level, with many of the main topics were discussed. For me, both the book’s discussion of the theoretical stuff and its application to real-life situation were interesting, but I would imagine even someone with a CS degree to the links that the authors build between the theory of algorithms and everyday life to be clever and insightful.
To someone coming from a purely non-CS background, I’d say this is actually one of the best currently available introductions to what algorithms are and how algorithmic decision-making works. I’ve already recommended it as such to students interested in computational social science, and I’d very much recommend it to anyone from the social science side of academia riding the current algorithm fad or considering hopping on that bandwagon.
Of the authors, Tom Griffiths is Professor of Psychology and Cognitive Science at Princeton, and Brian Christian is a writer with a background in philosophy, computer science and, interestingly, poetry. A bunch of other smart CS people appear in the book via quotations or citations.
* * *
It’s a sadly little-known fact that there exists an optimal algorithm for finding the best possible soulmate. It’s equally sadly little-known that even said algorithm cannot be guaranteed to give the best result even most of the time.
That result is related to an interesting decision-theoretic problem called the secretary problem, and its discussion forms the core of Algorithms to Live By‘s first chapter, which deals with optimal stopping. Let’s assume that you’re running a firm and want to hire a new secretary. You have n applicants to the position, and you know n; let’s say it’s one hundred. You can unambiguously rank the applicants from best to worst once you’ve seen them, and you interview them sequentially. After each interview, you can either accept an applicant or reject them – once rejected, and applicant can no longer be accepted.
Now, the problem is: how to ensure that you end up hiring the best possible applicant? The order in which the applicants come is random, so the best applicant can be the first one, the last one, or anything in between. If you pick the first, possibly very good, candidate, there’s a high probability that later on you would have met someone even better. But if you refrain from making a decision until the very end, it’s also extremely likely that you will end up passing by the best applicant.
The trick is that there is no way to be sure that you pick the best candidate, but there is an algorithm which guarantees that, as n grows, you have a 1/e or around 37% chance of choosing the best one (or, perhaps more accurately, an algorithm that, when used, will choose the best applicant 37% of the time). It’s a very simple one: reject each of the first 37% of applicants, then immediately choose the first one who’s better than any of the one’s you’ve seen before. Unfortunately even this algorithm misses the best applicant almost two-thirds of the time – but given that the assumptions hold, there’s no way to beat it.
The problem’s formulation is curiously ill-suited to the scenario that’s usually presented, in that job applicants are not generally accepted or rejected immediately after an interview. There are, however, real-life situations which closely resemble it – such as buying an apartment, or dating. In Western societies, it’s generally (after the early stages, at least) not acceptable to date multiple people simultaneously, and if you choose to reject a potential mate or break up with them, there’s commonly no coming back. So the problem of choosing whether to settle in with a person or keep looking in the hopes that there’s someone even better around the corner is something encountered by most people who are looking to commit themselves to a serious relationship.
Of course, the exact formulation of the question does not apply here, either. Certainly, the n of potential mates is rarely known with certainty (and for many people, almost certainly does not approach infinity). Ordering the prospective partners is also probably hard to do with certainty, although with a reasonably-sized n it can probably be done with some degree of accuracy. Here, Christian and Griffiths suggest reframing the problem a bit: choose a timeframe, say, five years or your twenties or thirties or whatever during which you want to find a partner. Then spend the first 37% of that dating without seriously considering committing and establishing a baseline. After that, settle in with the first one whom you’d rank higher than the best one you met during your wild years (and hope that they’re not in their baseline-estimation period, lest that the assumptions of our scenario will not hold and they will end up rejecting you instead).
This will yield a 37% probability that you settle in with the smartest, hottest, most warm-hearted one of all the people who agreed to date you. More likely you’ll pass them over and end up with whoever you met the last just before the end of your search period, someone who’s probably not as good as the One That Got Away. But at the very least you will be able to find solace in the fact that this was the best you could do. For a serial monogamist there’s no better algorithm, so you’ll need to settle for at best a 37% chance of finding the closest-to-the-right one – or maybe choose a different set of assumptions and start practicing polyamory or some other form of (hopefully ethical) non-monogamy.
* * *
Other chapters in the book deal with, for example, explore vs exploit problems, Bayes’ theorem, overfitting and game theory. The first half of the book deals more closely with everyday real-life situations. For example, chapter two on explore/exploit problems begins with a discussion of the awesomely named multi-armed bandit problem. That is, the problem of which slot machine to play at a casino, when the odds of each machine’s payoff are unknown, and the only way to gain that information about a machine is to play enough of it.
Again, there are real-life problems that are more familiar to those of us who do not frequent casinos, such as eating at restaurants. Each time you eat out, you have the option of exploiting your existing knowledge by going to a restaurant that you know for sure is great. But picking a safe choice every time entails accepting the risk that there’s an even better restaurant out there that you’ll never find out about because when you exploit, you can’t explore. Of course, when you explore, you’ll more likely than not end up eating at a place that’s sub-par.
Some practical recommendations emerge. For example, the authors (quite sensibly) point out that you’d do well to prioritize exploration when you’ve just moved into a city, and exploit when you’re about to leave. The value of any information obtained is, after all, tied to how long you will be able to use it. But the chapter also contains a very interesting discussion on the ethics of running clinical trials.
In a randomized controller trial that studies treatments to an illness, patients are split into groups and receive a different kind of treatment based on which group they were sampled into. Most likely, at least if it’s a study comparing new treatments to well-established ones, one of the treatments works better than the others. Sometimes it’s the new treatment, more often an old one. Knowledge of what treatment works best will probably emerge during the trial, but patients are generally given the same treatment for the entire duration of the study. This raises the obvious but (according to the authors at least; I don’t really know much about medicine myself) often neglected ethical problem that some patients in a study are given treatment that’s known (with some degree of certainty) to be worse than an alternative.
A possible solution, the authors suggest, is to treat clinical trials as multi-armed bandit problems and use an adaptive trial setup. This setup, introduced by the biostatistician Marvin Zelen, involves treating patients sequentially and goes roughly like this. First, pick a treatment at random for the first patient and see what happens. If the treatment is a success, increase the probability of that treatment being selected during subsequent trials; if not, increase the probability of the other treatment. (You can imagine there being two kinds of balls in an urn, one for each of the treatments, and picking a ball from it at random. At first there are two balls; each time a treatment is successful, add one ball of the corresponding kind to the urn.) That way, you’ll gain knowledge of the effectiveness of each treatment as the trial proceeds, and each patient will get treated according to the researchers’ best knowledge. The book discusses (classical) trials of an approach, called ECMO (that’s extracorporeal membrane oxygenation for you) to treating respiratory failure in infants, which was eventually deemed better than pre-existing treatments, but not until quite a few infants receiving ultimately inferior treatment had died during trials. Apparently there’s been a discussion in the medical community about whether it was ethical to assign patients into groups receiving inferior treatment even after preliminary evidence had surfaced that a better option was available.
I’m not sure how relevant all of this is. I kind of suppose that the authors are simplifying the issue quite a bit, and there are probably a bunch of medical scientists out there who object to this on some grounds. But I found this a fascinating idea nevertheless, and it’s an interesting direction to turn to from considering the classical multi-armed bandit problem.
Some other practical ideas contained in the book: it only makes sense to sort something, if it actually saves time. Interestingly, and I didn’t know this, there’s way to sort a bookshelf alphabetically in approximately linear time, or O(n) for short, using a technique called Bucket Sort, if you know beforehand how to sort the books into roughly even-sized categories that are needed as an intermediate step to full sort in this technique. However, just going through that bookshelf one by one can always be done in linear time, and that’s the worst case – usually, the book you want to find is not the last one on the shelf. (If you notice that that for some reason that’s the case, then you could of course leverage that information in how you search your bookshelf.)
I like to sort my bookshelf because I kind of enjoy having my books in certain order – standard-sized fantasy books at the beginning, followed by the few other kinds of fiction books that I own, them followed by a motley of non-fiction books, and finally, comics, video games, and so on. I do it every time I move and occasionally adjust it when I add new books – I rarely reread books, so after that, the shelf more or less remains untouched. I reserve the right to do this despite its irrationality because I like it.
But I did decide to stop caring about the order in my kitchen cabinet after reading Algorithms to Live By. Instead, I now just put the stuff that I regularly use at front of the cupboard – things like muesli, peanuts, textured soy protein and, well, muesli again. The stuff that I use less often gets pushed to the back of the cupboard, where it remains until I need it again, after which I put it in the front again. This sounds like an excuse for messiness (and to be honest, it probably is), but at least it’s rational messiness. I spend a lot less time worrying about placing everything where it needs to be and usually find everything immediately when I need it.
* * *
Algorithms to Live By gets a lot more philosophical towards the end. The first few chapters do occasionally mention things such as the multi-armed bandit implying that life should get better as you age – after all, when you’re old, you can focus on exploiting a lifetime of wisdom and need to care less about exploring. But the latter half seemed to me to focus a lot less on practical problems like finding a free parking space, and a lot more on more fundamental topics.
A recurring theme here is the huge computational challenge of modelling a world in detail, and the folly of trying that with a puny human brain (or, indeed, any computer). The chapter on overfitting explicitly warns about thinking too much, noting that it may well lead to worse, not better, decisions than acting on instinct. For those of you not versed in the language of statistical models, overfitting happens when you build a complex model based on a set of observations, and that model ends up sucking at predicting new observations because it’s too sensitive to random variations in the training data set. Like in this example, from Wikipedia:
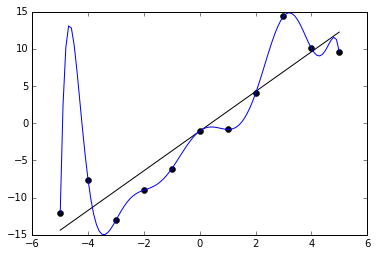
CC BY-SA 4.0 Ghiles (source)
The blue line represents a hugely complicated model that perfectly “predicts” the placement of each black dot in the graph, much better than the very simple model represented by the black line. But it’s obvious that the black line is much better in reality – just imagine adding a new data point with x = 6, and try to figure out where the blue model and the black model would expect it to appear.
I’m very happy that overfitting has its own chapter in this book, because the need to avoid overfitting when making decisions is something that I’ve thought a lot about myself – and often failed terribly at. Overfitting is why one probably shouldn’t be a classical utilitarian on a daily basis – the complexity of figuring out exactly what to do in a situation with a huge set of factors that should theoretically be taken into account is far too overwhelming, and trying to do make a decision based on, say, wanting to minimize a specific person’s suffering based on how you expect their mind to work and react in a specific situation will probably lead one completely astray. Better by far to adopt a deontological or, perhaps, a rule-based utilitarian approach. If you go by well-accepted norms, do your best to avoid killing anyone and try not to lie too much, you’ll probably do quite well. You will make mistakes, of course, but I bet that they will be less disastrous.
The chapters on randomness and relaxation go further into this, dealing more with the fundamental complexity of the world, and how finding perfect answers to computational problems is often impossible in practice. These contain some of the deepest insights this book has to offer, which happen to be some of the most fascinating ideas that I have encountered while studying computer science.
Roughly speaking, it’s this: the world we live in is in very many ways computational – a case has been made that it’s fundamentally so. The authors cite Scott Aaronson, who points out that the quantitative gaps in problems of different complexity classes in computer science are effectively qualitative gaps. As Aaronson has pointed out, for example, finding out that P equals NP – a famous and unsolved puzzle in computer science – would, in a sense, imply that there’s no fundamental difference between appreciating a great book and writing one.
Computational complexity offers one perspective to appreciating what this fundamental difference is. And it’s not immediately obvious. A few months ago, an acquaintance of mine talked about how fascinating it would be to have a library that contains every book that can be written. Sadly, I was not clever enough back then to boast that I happen to have just such a library on my computer (at least one that contains all books made up of Unicode characters that fit in approximately 16 GB of memory), and that he just needs to figure out a way to find the books he’d like to read from it.
But it also details how it’s often surprisingly easy to find answers that are good enough to problems in NP. Solving the traveling salesman problem is intractable to even the most powerful number-crunchers on this planet with just a few dozen cities in the salesman’s graph. But it can be solved, the book points out, if you’re satisfied with a solution that’s within less than 0.05% of the optimal solution – which, I would imagine, is quite enough in most situations.
The chapter on Bayes’ rule contains some similar insights, as it focuses a lot on the Copernican Principle and details J. Richard Gott’s famous prediction that the Berlin Wall would fall before 1993 with 50% probability. Gott’s reasoning was based on him seeing the Wall in 1969, eight years after it was built, and noting that he should expect to be there at the wall at roughly the mid halfway point of its lifetime. Thus, Gott surmised, the wall should stand for about another eight years – and, considering that the Wall might have stood for 8000 years like namesake in Westeros, his guess was pretty good.
Of course, someone using this logic and looking at the Notre-Dame in March 2019 would have expected the cathedral to remain standing for approximately 700 years more. Still, the general principle is valid. In itself, it’s also probably already familiar to many of you. What was interesting in Algorithms to Live By’s treatment of the topic was their discussion of how the Copernican Principle behaves with different kinds of priors. The example with the Berlin Wall is based on using an uninformative prior – every lifetime for the Wall is, a priori, assumed to be equally likely. However, we probably have better priors than that in many cases. How much money films make to their producers, for example, follows a power-law distribution. To predict how much money a film makes over its lifetime, you should take its current earnings and multiply them by a constant amount (according to the authors, this constant happens to be 1.4). (What I should expect my h-index to grow up to by this logic I dare not think of.) For a phenomenon following a normal distribution, predict the average of that distribution. And so on. As unintuitive as this logic appears at first, I think it’s quite fascinating that accurate predictions can be made with hardly any information. And yet it’s also quite intuitive: after all, if you wanted to find someone’s number from the phone book, back in the days when they still existed, you probably started your search by opening it roughly from the middle.
* * *
I did not like all of Algorithms to Live By. For one, I think it’s latter half wasn’t written with the same meticulousness as its beginning. And although its more philosophical aspects were interesting, it did feel like the authors were trying to cram a lot of points in a relatively short books, and weren’t that careful with all of them. The books penultimate section on game theory, for instance, besides featuring a fascinating discussion of the fact that finding a Nash equilibrium is an NP-complete problem (I wonder what economists have made of that), goes to discuss norms and religion as solutions to game-theoretic coordination problems. It also discusses the feeling of romantic love as a way to avoid a Prisoner’s Dilemma in coupling.
This is not wrong – it highlights the fact that people willing to form a relationship need to be able to be reasonably sure that their partner will be faithful, and to be able to signal their own faithfulness as well. When dealing with a creature that can read your mind, it helps a lot in being able to signal your faithfulness if you are indeed faithful. But still, this is hardly the end of the story – as Kevin Simler and Robin Hanson point out, the fact that your conscious motivations are pure does not mean that your real motivations are, too. Even with romantic feelings in place as a coordinating mechanism, the temptation to defect is still there. This does feel a bit like computer scientists using their favourite tools to explain the world, and doing it a bit lazily. Maybe they didn’t intend it that way.
Nevertheless, I think Algorithms to Live By is a great book, and besides some minor complaints like that, I don’t have many. It’s one part handy life advice, one part good introduction to the theory of computation, one part enjoyable armchair philosophy. Regardless of your background, I believe you would be a wiser person if you read it.